Jian Yang's Hotdog App; The CogSci Approach
Human inductive bias, few-shot learning, and the food hyperplane
This post ends a recent series of posts on the topic of inductive bias in machine learning.
Grey swans, and what a bit of linguistics can teach you about machine learning
Inductive bias and why overfitting a 1/2 trillion words looks sexy
Here we continue with a discussion on the subject of Bayesian concept learning and explanations.
Few-shot learning in the human head
Humans can do a cool trick when it comes to learning new concepts. Firstly, they can learn from just a few examples, what machine learning folks call few-shot learning. Secondly, they don't seem to need many negative examples.
For instance, when you introduce the concept of a hotdog to a child, they seem to catch on without you showing them examples of non-hotdogs. To be clear, showing them some negative examples helps refine the hotdog concept but doesn't seem to be needed to reach good generalization performance.
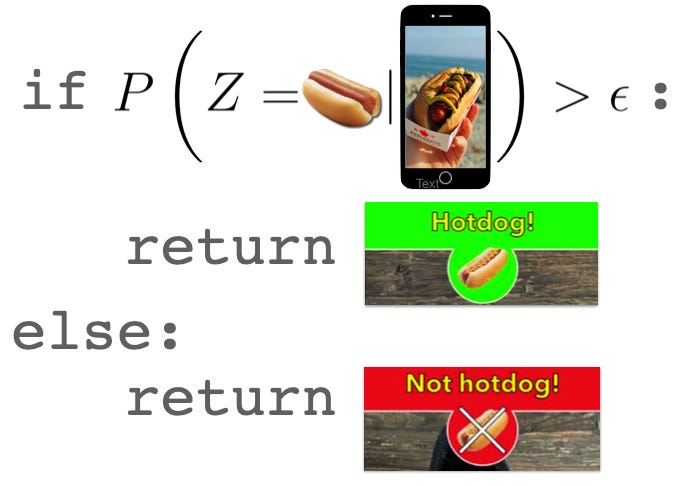
I can't use the hotdog analogy without referencing the gag on the comedy show Silicon Valley that spawned it. The character Jian Yang develops a machine learning-driven mobile app that can seemingly return the correct text-name of the food in a camera picture. He demonstrates the app by taking a picture of a hotdog, and the algorithm returns "Hotdog."
The other characters are excited about owning a piece of what promises to be the “Shazam for food”. However, when they have him try it on a slice of pizza, instead of returning "Pizza," the algorithm returns "Not Hotdog."
The team is disappointed, and the audience has a laugh. It gets interesting after the character Dinesh points out that the algorithm works, Jian Yang "just" needs to get it to work for other foods.
Monica (sardonically): So what he did for hot dogs, he needs to do for every food in existence.
Jian Yang: No! That's very boring work. That's scraping the internet for thousands of food pictures. You can hire someone else.
Finding and labeling data is expensive, at the very least in terms of labor. There is a global economy of gig workers who you can pay to apply labels to image datasets, such as pictures aspiring Instagram celebrities take of their meals. Companies like Appen have built big businesses in this gig economy.
In economic terms, we can characterize the few-shot positive-example learning ability as something that would make creating Jian Yang's Shazaam for food much easier in terms of saved personal labor or expense on gig labor.
Machine learning researchers are also well aware few-shot learning is a challenge, particularly with deep learning's need to be trained large data, and it’s an active area of research.
However, they tend to pay less attention to reducing reliance on negative examples. This lack of awareness is because, in practical terms, getting examples of "not the thing you care about" is often easy. But for nuanced problems, you don’t just want any negative example; you want "almost the thing you care about but not quite." For example, when you seek negative examples to help that child refine their understanding of the concept of hotdog, you explain how an Italian sausage is not a hotdog, not how ice cream is not a hotdog. This type of negative example can be harder to acquire, even when you have access to big data.
Jian Yang articulates this point perfectly in the latter part of the episode, where he’s clearly tired with feeling around for the borders of what makes a hotdog a hotdog.
I f*ing hate Seefood. I have to look at different hotdogs! There’s Chinese hotdogs, Polish hotdogs, Jewish hotdogs, it’s f*ing stupid!
[Note: It is only now, knowing the conclusion of this plotline, that I get the double entendre. Hard eyeroll 🙄.]
How machine learning models approach learning from positive examples
Let's evaluate some machine learning paradigms on how well they approach a human's ability to work with a small set of positive examples.
Imagine there is a hyperplane of food, where each food concept occupies some specific region in this space. There is a hotdog region in this space. Every food that is a hotdog maps to some point in this hotdog region of food hyperplane.
Some machine learning approaches focus on learning the border that separates hotdog regions from other regions of space. It takes an image, maps it to either side of that border, and returns "hotdog" if the image falls on the right side of the hotdog border.
Some models use probability-based methods. For example, they might model the log value of likelihood, as in how likely coming from hotdog space is the reason an image of a food item looks the way it does.

Bayesians take a converse approach that is only subtly different in language; they'll model the probability the item is from hotdog space, given the evidence of the image.
Either way, we get a bit closer to focusing only on positive examples because positive examples alone are all we need to get both likelihood and Bayesian probability models. However, many probability-based methods still rely on thresholding to decide in the end whether or not it is a hotdog; they conclude the image is a hotdog if the likelihood or Bayesian probability exceeds some threshold “ε”.
Finding a threshold “ε” that maximizes predictive accuracy requires negative examples.
But we can get around this quickly enough. We only need to build probability models for each distinct food region of the food hyperplane and choose the region that maximizes the likelihood or posterior probability for a given image.
The hard part: how do we get a probability model of the food hyperplane?
So the question is, how does our probability model represent the hotdog region of the food hyperplane? A standard deep computer vision architecture would describe the space in terms of a hierarchy of color patterns and geometric shapes.
In a previous post, I described some of the inductive biases common in popular deep computer vision architectures (e.g., invariance to translation).
Humans don’t think about food this way. To emulate the ability to achieve few-shot learning with positive examples, we could look to cognitive science.
Cognitive science research suggests human inductive biases are motivated by theories of the domain. By "theory," I mean a set of related abstractions subject to causality-based rules and relational constraints. Examples include:
Bread usually wrap meats, but meats rarely wrap bread.
Hotdogs can go without toppings, even a bun, but can't go without a frank. But a hotdog with a meat-free frank is still a hotdog.
Liquids take the shape of their container.
Lightly burning bread or a sugary custard will create a pleasant brown exterior.
Such rules and relationships constrain the probability models of the food regions. To use machine-learning-speak, causal rules and relational constraints provide an inductive bias. So how do humans decide which causal rules and relational constraints to go for?
Explanations, taxonomies, conversations, and probability
Cognitive science researchers argue that probabilistic reasoning in humans relies on explanations, not just correlation. For example, when we talk in probabilistic terms about how likely coming from hotdog space is the reason an image of a food item looks the way it does; we'd explain it as "The item that is most likely to produce this image of what looks to be a bun with a frank in it would be a hotdog, because a hotdog is a frank in a bun (duh)."
Researchers have had a tough time nailing down the definition of explanation with enough mathematical precision to make it clear how to implement in software, though causal inference researchers have tried (Halpern and Pearl, 2005). The difficulty is likely due to their being a conversational element to explanation; the hotdog-likelihood embodies a pragmatic assumption that the concept of hotdog will be shared with a future conversational interlocutor (Bloom 2000, Kirfel and Icard 2020).
Research also shows human cognition organizes object-kind concepts into fuzzy tree-structured taxonomies with labels at various levels (Tenenbaum, Griffiths, and Kemp 2006). The contents of the person’s trees vary depending on that person’s experience. When I think about where in my food taxonomy hotdogs live, I think it might be something like this:
When humans learn a new object kind, they assume the teacher is focusing on the bottom of the tree rather than the middle. That assumption constrains Bayesian “prior” probability.
For example, if I present a plate containing a warm hotdog with mustard and tell a child, “here’s some food called a hotdog!”,
the child will assume the concept of "hotdog" encompasses a specific food item on a hypothetical menu, rather than all plate-ready food-things, warm things, or all foods topped with mustard.
Full disclosure, I’m one of those machine learning experts in the neurosymbolic camp; people who are excited about deep learning’s advances, and thinks there are some major breakthroughs to be made by combining DL with formal causal inference, cognitive science, linguistics, formal grammars, etc.
Do you like these cog-sci-flavored posts? Like below or share with a friend so I know to write more of these in the future.
Go Deeper
Halpern, J. Y., & Pearl, J. (2005). Causes and explanations: A structural-model approach. Part II: Explanations. The British journal for the philosophy of science, 56(4), 889-911.
Kirfel, L., Icard, T. F., & Gerstenberg, T. (2020). Inference from explanation. PsyArXiv.
Lombrozo, T. (2006). The structure and function of explanations. Trends in Cognitive Sciences, 10(10), 464-470.
Tenenbaum, J. B., Griffiths, T. L., & Kemp, C. (2006). Theory-based Bayesian models of inductive learning and reasoning. Trends in cognitive sciences, 10(7), 309-318.